Regularization

Introduction

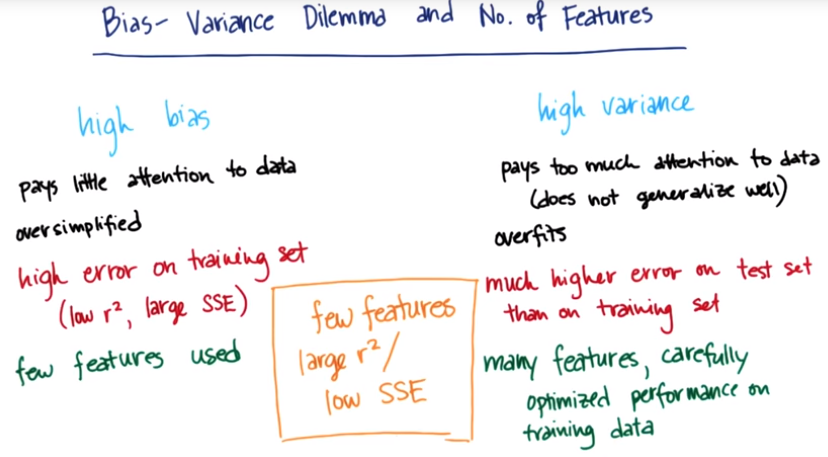
Regularization is a technique that applies to objective functions in ill-posed problems formulated as optimization problems or to prevent overfitting.

The bias-variance tradeoff (or dilemma) is the problem of simultaneously minimizing two sources of error that prevent supervised learning algorithms from generalizing beyond their training set:

The bias is error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs, underfitting.

The variance is error from sensitivity to small fluctuations in the training set. High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs, overfitting.

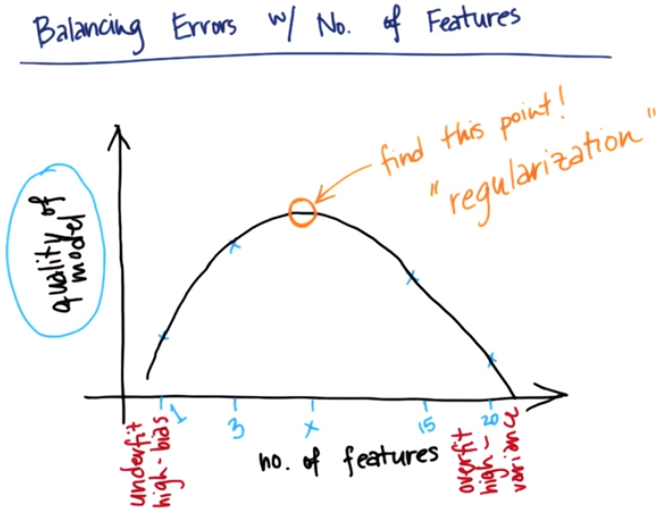
It's a way to balance the errors given by the regression with the number of features that are required to get those errors. With only one feature in the model, the likelihood of underfitting the data is pretty high. Allowing more features that are good at describing the patterns in the data brings the error down because the model is now fitting the data in a more precise way. However, bringing more features to the model makes it more susceptible to overfitting and actually lower the quality of the model, giving this arc shape. The process of regularization consist of mathematically define what the maximum point is. Some algorithm can trade off between the precision, the goodness of fit, the very low errors, and, the complexity of fitting on lots of different features.

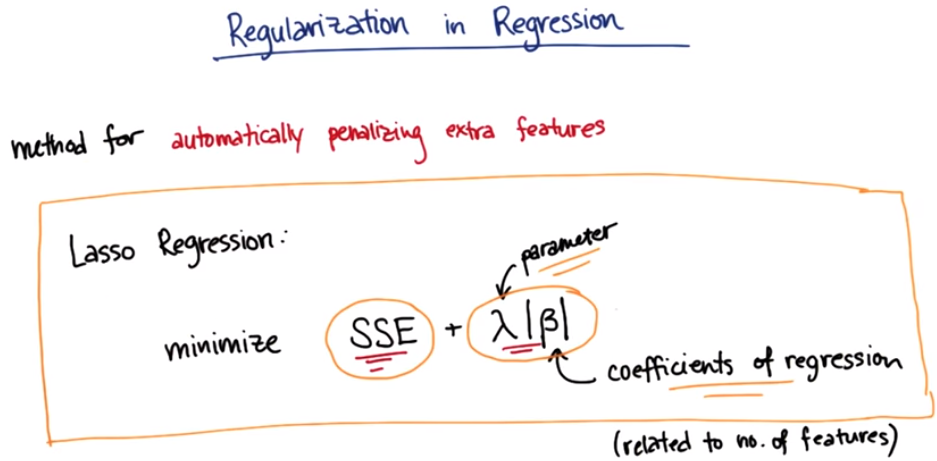
One very powerful place that you can use regularization, is in regression. Regularization is a method fo automatically penalizing the extra features that you use in your model. There's a type of regularized regression called Lasso Regression and, here's the rough formula for the Lasso Regression . In a regular linear regression we want to minimize the sum of the squared errors (SSE) in the fit (the squared distance between the fit and any given points). Lasso Regression selects for the smallest sum of squared error in addition to minimizing the number of used features. The second term, including the penalty parameter λ and the coefficients of the regression β, describes how many features are used. When performing a fit, both the errors that come from that fit, and also the number of features that are being used are considered. Adding more features might lead to a lower SSE but for each extra feature a penalty is added along with the coefficients of regression. Therefore the gain, in terms of the precision, the goodness of fit of the regression, has to be a bigger gain than the loss of having that additional feature in the regression. The Lasso regression figures out which features have the most important effect on the regression and set to zero the coefficients for the features that basically don't help.

Regularization in the Enron Corpus

Enron was one of the largest US companies in 2000. At the end of 2001, it had collapsed into bankruptcy due to widespread corporate fraud, known since as the Enron scandal. A vast amount of confidential information including thousands of emails and financial data was made public after Federal investigation.

In this project, Lasso regression will be used to determine which features are the most important

We first need to download the Enron Corpus (this might take a while, like more than an hour) and unzip the file (which can take a while too). There is 156 people in this dataset each one identified by their last name and the first letter of their first name.

Let's take a look at the data. The dataset for the project can be read as a dictionary where each key is a person and its value is a dictionnary containing all the possible feature. Here is an example of one of the entry :

                                        
{'ALLEN PHILLIP K': {'bonus': 4175000,
'deferral_payments': 2869717,
'deferred_income': -3081055,
'director_fees': 'NaN',
'email_address': 'phillip.allen@enron.com',
'exercised_stock_options': 1729541,
'expenses': 13868,
'from_messages': 2195,
'from_poi_to_this_person': 47,
'from_this_person_to_poi': 65,
'loan_advances': 'NaN',
'long_term_incentive': 304805,
'other': 152,
'poi': False,
'restricted_stock': 126027,
'restricted_stock_deferred': -126027,
'salary': 201955,
'shared_receipt_with_poi': 1407,
'to_messages': 2902,
'total_payments': 4484442,
'total_stock_value': 1729541}
}

Then the data are converted from the dictionary to a list that's ready for training.

                                
### Modified from: Udacity - Intro to Machine Learning

import pickle
from feature_format import featureFormat, targetFeatureSplit

##########################################################################
### Split data

### A pickle document was created by the instructors of the course.
### To find it, see the full project on github
dictionary = pickle.load( open("../final_project/final_project_dataset_modified.pkl", "r") )

poi = 'poi'

feature1 = 'bonus'
feature2 = 'deferral_payments'
feature3 = 'deferred_income'
feature4 = 'director_fees'
# feature5 = 'email_address'
feature6 = 'exercised_stock_options'
feature7 = 'expenses'
feature8 = 'from_messages'
feature9 = 'from_poi_to_this_person'
feature10 = 'from_this_person_to_poi'
feature11 = 'loan_advances'
feature12 = 'long_term_incentive'
feature13 = 'other'
feature14 = 'restricted_stock'
feature15 = 'restricted_stock_deferred'
feature16 = 'salary'
feature17 = 'shared_receipt_with_poi'
feature18 = 'to_messages'
feature19 = 'total_payments'

features_list = [poi, feature1, feature2, feature3, feature4, feature6,
feature7, feature8, feature9, feature10, feature11, feature12,
feature13, feature14, feature15, feature16, feature17, feature18,
feature19]

data = featureFormat(dictionary, features_list)
labels, features = targetFeatureSplit(data)

regression = Lasso()
regression.fit(features, labels)
print (regression.coef_)

>>> Should print:
[2.94719813e-07     2.80116288e-07      1.39812028e-07      2.63442675e-08
1.75981543e-08      1.18020582e-06      -1.08723530e-05     2.81688787e-05
7.08389481e-04      -2.04321488e-07     3.11124785e-07      3.81194048e-07
-1.21136270e-08     3.38544287e-07      6.25902867e-07      1.71456804e-04
-7.22776730e-05     -3.50369452e-07]

Feature	Score
bonus	2.94719813e-07
deferral_payments	2.80116288e-07
deferred_income	1.39812028e-07
director_fees	2.63442675e-08
exercised_stock_options	1.75981543e-08
expenses	1.18020582e-06
from_messages	-1.08723530e-05
from_poi_to_this_person	2.81688787e-05
from_this_person_to_poi	7.08389481e-04
loan_advances	-2.04321488e-07
long_term_incentive	3.11124785e-07
other	3.81194048e-07
restricted_stock	-1.21136270e-08
restricted_stock_deferred	3.38544287e-07
salary	6.25902867e-07
shared_receipt_with_poi	1.71456804e-04
to_messages	-7.22776730e-05
total_payments	-3.50369452e-07